2024. 5. 26. 20:11ㆍ알고리즘 이론
1. 동적 계획법이란?
동적 계획법이란 해결하고자 하는 문제를 작은 문제로 나누어 해결하고, 작은 문제들의 해들로부터 큰 문제의 답을 구하는 방식입니다. 여기서 중요한 점은 "분할과 정복"과 달리 DP는 분할된 작은 문제들이 상호 독립적이지 않고, 일정 부분을 공유한다는 점입니다.

본인은 편의점 알바를 하고있습니다. 그리고 저는 항상 출근하면 가장 먼저 담배 재고를 조사합니다. 담배를 꺼내 세다보면 맨 오른쪽처럼 10개가 넘어가는 재고들이 종종 있는데, 이런 경우에는 한눈에 몇개인지 들어오지도 않고 이런 것들을 하나하나 다 세다보면 재고 조사에 쓰는 시간이 꽤 길어집니다. 그렇다고 대충 눈대중으로 세고 넘어가기에는 여간 찝찝한게 아니죠.

사진 속 모든 담배의 개수를 세야한다고 가정해볼까요?

세줄로 나누어 세는 것이 작은 문제로 나누어 해결하는 걸로 볼 수 있겠네요.

그리고 담배의 크기가 일정하여 같은 줄에 있다면 개수가 같다는 것을 알고 있습니다.
각 줄의 담배 개수에 대한 정보를 일정 부분 공유한다고 볼 수 있겠습니다.

때문에 첫번째 줄에서 센 개수를 두번째 줄에서 재사용하면 한개만 더세어서 두번째 줄의 담배 개수를 구할 수 있습니다.
마찬가지로 세번째 줄의 담배 개수는 두번째 줄에서 구한 개수에 3개만 더 구하면 됩니다.
2. Top-Down (Memoization) / Bottom-Up (Tabulation)
동적 계획법은 하향식 계획법(Top-down)과 상향식 계획법(Bottom-Up)으로 나뉩니다.
Top-Down (Memoization)
하향식 접근법(Top-Down, Memoization)은 가장 큰 문제에서 시작하여 재귀적으로 더 작은 하위 문제로 나눕니다. 그리고 중복 계산을 피하기 위해 해결된 하위 문제의 결과를 메모이제이션 테이블에 저장합니다.
우리들이 사랑하는 피보나치 수열로 예를 들어보겠습니다.

단순히 재귀함수로 Fibonacci 수열을 구현했을 때는 위 트리 구조와 같이 값을 구하는데 불필요한 중복된 호출이 발생합니다.

하지만 만약 처음 F2를 구하는 과정에서 이를 따로 기록해 두었다면, 두번째 F2를 구하는 과정에서는 F1과 F0을 재귀호출하는 것을 미리 구해둔 값을 참조하는 것으로 대체할 수 있게 됩니다.
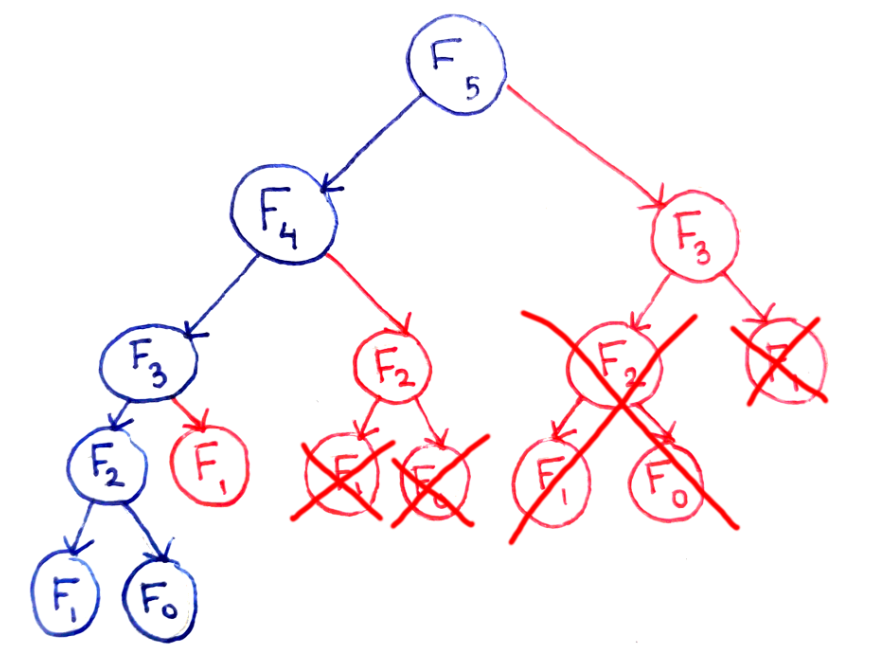
이렇게 하위 문제에서 구한 값을 저장하는 것이 메모이제이션이며, 이를 사용해 불필요한 중복 호출을 방지하는 것이 동적 계획법의 하향식 기법(Top-Down)입니다.
이를 코드로 구현해보면 다음과 같습니다.
function fibonacciTopDown(n, memo = {}) {
if (n <= 1) return n;
if (memo[n]) return memo[n];
memo[n] = fibonacciTopDown(n - 1, memo) + fibonacciTopDown(n - 2, memo);
return memo[n];
}
// 사용 예시
console.log(fibonacciTopDown(10)); // 출력: 55Bottom-Up (Tabulation)
상향식 접근법(Bottom-Up, Tabulation, 즉 타뷸레이션에서는 작은 하위 문제부터 시작하여 점차 큰 문제를 해결해 나갑니다. 이는 주로 반복문을 사용하여 구현되며, 하위 문제의 해결책을 테이블에 저장하면서 점진적으로 최종 해결책을 찾는 방식입니다. 맨처음 예로 들었던 담배 재고 조사도 상향식 접근법으로 볼 수 있습니다.
마찬가지로 피보나치 수열을 예로 들어보겠습니다.
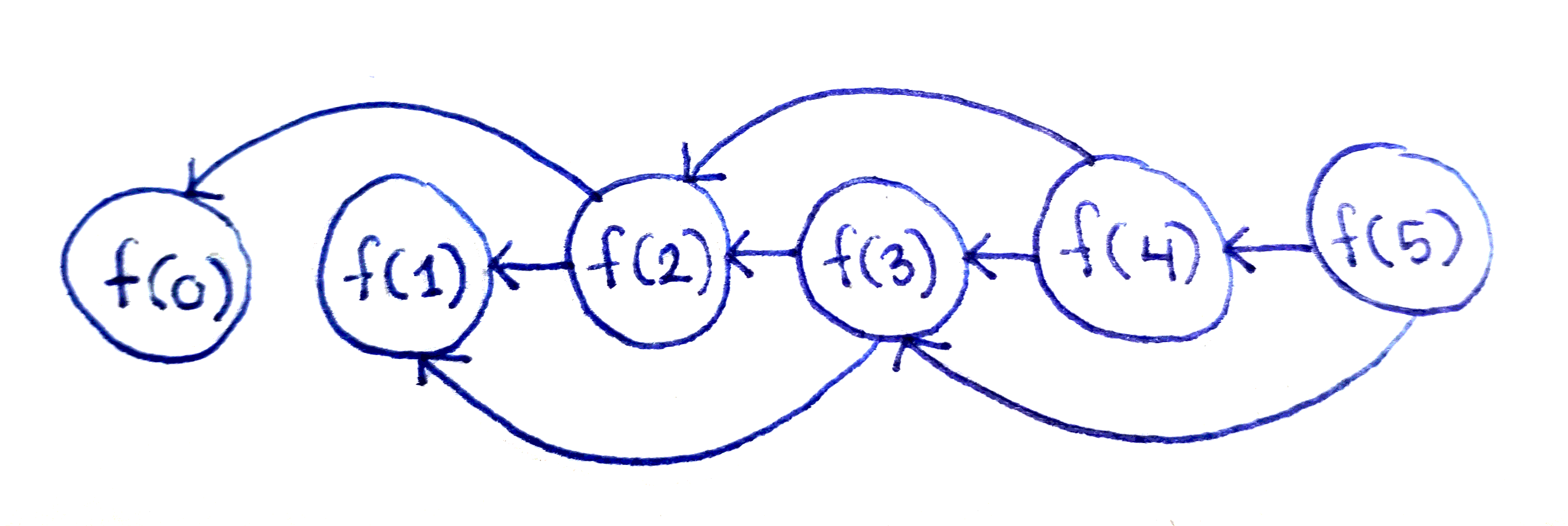
f(0)에 0이, f(1)에 1이 저장된 상태로 시작한다고 하면, f(2)는 f(0)과 f(1)을 더하면 되고, 그 다음 f(3)은 이전에 구한 f(2)와 f(1)을 더하면 됩니다.
f(n)이 참조하는 값이 f(n-1)과 f(n-2)이기 때문에 위 그림에서 화살표가 왼쪽으로 향하듯이 표현되어 있지만, 실제로는 반복문을 통해 n값이 1씩 증가하고 있기 때문에 테이블에 값이 저장되는 순서는 f(2) -> f(3) -> f(4) -> f(5)로 진행되고 있습니다.
상향식 기법은 이렇게 작은 하위 문제부터 시작하여 큰 문제를 해결해 나가는 양상입니다.
마찬가지로 코드로 구현해보면 다음과 같습니다.
//상향식 기법
function fibonacciBottomUp(n) {
if (n <= 1) return n;
let fib = [0, 1];
for (let i = 2; i <= n; i++) {
fib[i] = fib[i - 1] + fib[i - 2];
}
return fib[n];
}
// 사용 예시
console.log(fibonacciBottomUp(10)); // 출력: 55
//이전 하향식 기법
function fibonacciTopDown(n, memo = {}) {
if (n <= 1) return n;
if (memo[n]) return memo[n];
memo[n] = fibonacciTopDown(n - 1, memo) + fibonacciTopDown(n - 2, memo);
return memo[n];
}
// 사용 예시
console.log(fibonacciTopDown(10)); // 출력: 553. Top-Down (Memoization) VS Bottom-Up (Tabulation)
Top-Down (Memoization)
대부분의 경우 하향식 접근 방식(Top-Down)은 단순히 재귀 동작 중에 결과를 저장하고 이 값을 사용할 일이 있으면, 재귀 호출을 대신해 이 값을 참조하면 되기 때문에 구현하기 쉽습니다.
하지만 하향식 접근 방식(Top-Down)은 재귀 호출의 오버헤드로 인해 상향식 접근 방식보다 느리고, 콜스택 메모리도 차지하기 때문에 재귀트리가 매우 깊어지면 메모리 초과로 프로그램이 중단될 수도 있다는 문제점이 있습니다.
Bottom-Up (Tabulation)
상향식 접근 방식(Bottom-Up)은 추가적인 재귀 호출 스택이 없어 메모리 효율로 보나 처리시간으로 보나 일반적으로 하향식 기법(Top-Down)보다 효율적입니다.
하지만 앞서 말했듯이 작은 문제 단위에서 더 큰 문제의 해결로 나아가기 때문에, Top-Down과 달리 해당 문제의 규칙성을 찾아야 한다는 어려움이 있습니다. 다시 Fibonacci 수열을 예로 들면, Bottom-Up으로 이를 해결하기 위해서는 F(n) = F(n-1) + F(n-2) 라는 점화식을 세워야 한다는 것입니다.
이상으로 동적 계획법(Dynamic Programming)의 기본적인 내용들을 알아봤습니다. 감사합니다.
'알고리즘 이론' 카테고리의 다른 글
| LCS 알고리즘 (0) | 2024.05.24 |
|---|---|
| 너비 우선 탐색(BFS)와 깊이 우선 탐색(DFS) (0) | 2024.05.18 |
| 재귀 함수 (recursive function) 의 동작 (0) | 2024.04.13 |
| 그래프 ( Graph ) 탐색 이론 (1) | 2024.03.29 |