2024. 3. 29. 19:12ㆍ알고리즘 이론
1. 그래프의 구성요소
그래프의 기본 구성 요소는 정점(Vertex, 혹은 노드(Node))과 간선(Edge)입니다.
정점은 그래프의 기본 단위로, 위치나 상태 등을 나타낼 수 있고,
간선은 두 정점을 연결하는 선으로, 두 정점 사이의 관계를 표현합니다.
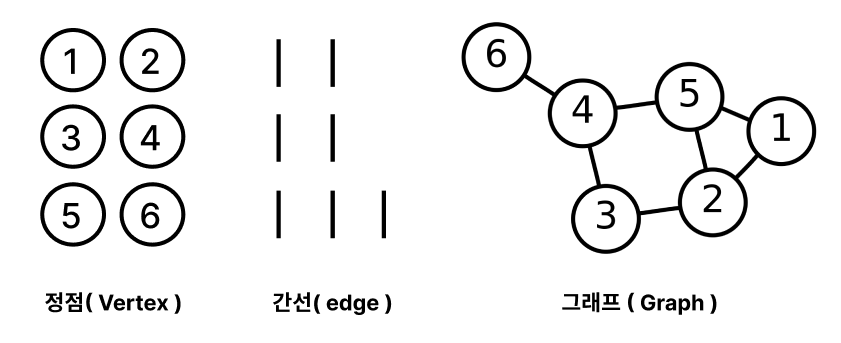
이러한 구성 요소들을 바탕으로, 그래프는 복잡한 네트워크 관계를 모델링하는 데 사용됩니다.
2. 그래프의 형태
그래프는 크게 방향성의 유무와 가중치의 유무에 따라 분류할 수 있습니다.
2-1. 무방향 그래프, 방향 그래프
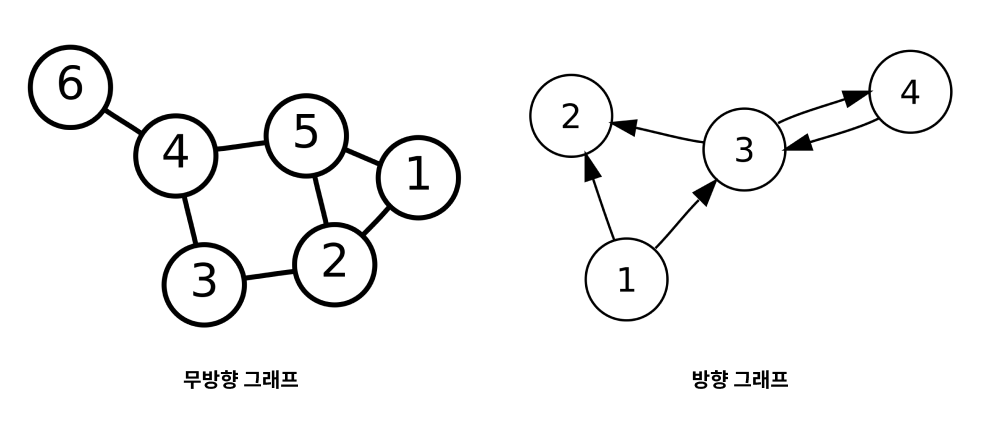
- 무방향 그래프(Undirected Graph): 간선에 방향성이 없는 그래프로, 간선이 (A, B)라면 A와 B는 서로 연결되어 있음을 나타냅니다.
- 방향 그래프(Directed Graph): 간선에 방향성이 있는 그래프로, 간선이 (A, B)라면 A에서 B로의 관계를 나타내며, B에서 A로는 나타내지 않습니다.
2-2. 비가중치 그래프, 가중치 그래프
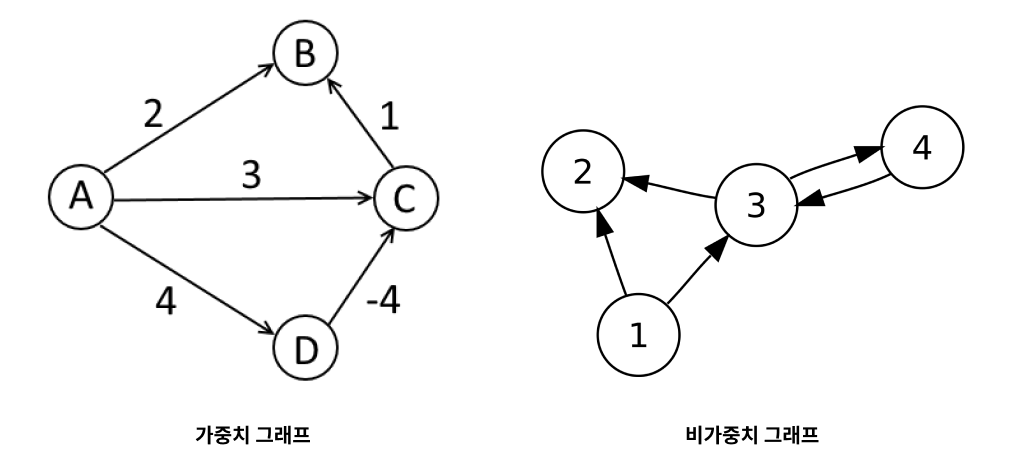
- 비가중치 그래프(Unweighted Graph): 모든 간선의 가중치가 동일한 그래프로, 가중치를 고려하지 않습니다.
- 가중치 그래프(Weighted Graph): 간선에 가중치가 부여된 그래프로, 두 정점 사이를 연결하는 간선에 특정 값을 할당할 수 있습니다. 이 가중치는 거리, 비용 등을 나타낼 수 있습니다.
여기까지 이해하셨다면, 그래프는 아래 4가지 형태가 나올 수 있다는 것을 알 수 있을겁니다.
- 가중치가 없는 무방향 그래프
- 가중치가 없는 방향 그래프
- 가중치가 있는 무방향 그래프
- 가중치가 있는 방향 그래프
만약 그래프를 처음 접하셨다면, 개인적으로 1. 가중치가 없는 무방향 그래프를 다루는 문제들을 풀어보며 입문하시는 것을 추천드립니다.
3. 그래프의 구현 방법
그래프는 주로 두 가지 방법으로 구현됩니다: 인접 리스트(Adjacency List), 인접 행렬(Adjacency Matrix)
3-1. 인접 리스트(Adjacency List): 각 정점에 대해 해당 정점과 인접한 정점들의 리스트를 저장하는 방식입니다. 인접 리스트는 메모리를 효율적으로 사용하며, 특히 희소 그래프(Sparse Graph, 즉 간선의 수가 정점에 비해 상대적으로 적은 그래프)에서 유리합니다.
3-2. 인접 행렬(Adjacency Matrix): 정점의 개수에 따라 2차원 배열을 생성하고, 배열의 각 요소는 두 정점 사이의 간선의 유무(무방향 그래프)나 방향, 가중치(방향 그래프, 가중치 그래프)를 나타냅니다. 인접 행렬은 구현이 간단하고, 모든 연결 정보를 빠르게 조회할 수 있는 장점이 있으나, 메모리 사용량이 정점의 수의 제곱에 비례하여 증가하는 단점이 있습니다.
설명만으로는 부족한 느낌이니 아래 그래프를 예시로 직접 구현해보겠습니다.
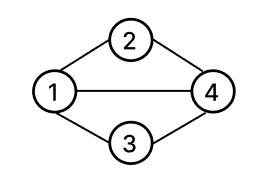
위와 같이 생긴 그래프 무방향 비가중치 그래프를 예시로 인접 리스트와 인접 행렬을 각각 사용해서 구현해보겠습니다.
입력은 서로 연결된 노드 한쌍을 한줄로 받고 있다고 하겠습니다.
3-1. 인접 리스트(Adjacency List)
/*
입력
1 2
1 3
1 4
2 4
3 4
*/
input.forEach(([from, to]) => {
graph[from].push(to);
graph[to].push(from); // 무방향 그래프이므로 양방향으로 추가
});
graph.forEach((g) => g.sort((a, b) => a - b));
console.log(graph.map((item, index) => `정점 ${index} : ` + item.join(" ")).join("\n"));
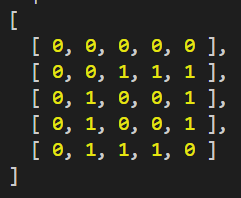
위 코드를 실행해보면 아래와 같은 출력이 나오게 됩니다.

인접 리스트에서 배열의 index는 각 정점( 1, 2, 3, 4 )들을 뜻합니다.
그리고 연결되어 있는 정점(index)들을 해당 정점에 배열 형태로 저장하고 있는 방식으로 정점간의 연결 즉, 간선을 표현합니다. 때문에 아래와 같은 2차원 배열 형태를 띄게 됩니다.

3-2. 인접 행렬(Adjacency Matrix)
const fs = require("fs");
const input = fs
.readFileSync("../input.txt")
.toString()
.trim()
.split("\n")
.map((item) => item.split(" ").map((item) => Number(item)));
const [N, M] = input.shift();
// 인접 행렬을 초기화합니다. 모든 값을 0으로 설정합니다.
const graph = Array.from(Array(N + 1), () => Array(N + 1).fill(0));
input.forEach(([from, to]) => {
graph[from][to] = 1; // 정점 from에서 to로의 연결을 표시합니다.
graph[to][from] = 1; // 무방향 그래프이므로, 반대 방향도 표시합니다.
});
console.log(' ', ...Array.from({length: N}, (_, i) => i + 1).join(''));
console.log(' ' + '-'.repeat(N * 2));
graph.slice(1).forEach((row, i) => {
console.log(`${i + 1} | `, row.slice(1).join(' '));
});위 코드를 실행해보면 아래와 같은 출력이 나오게 됩니다.
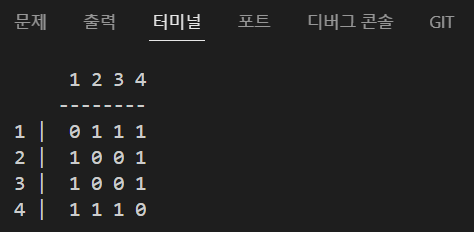
인접 리스트와 마찬가지로 인접 행렬에서 배열의 index는 각 정점( 1, 2, 3, 4 )들을 뜻합니다.
하지만 인접 리스트와 달리, 인접 행렬은 1차원 배열속 2차원 배열의 index들 또한 각 정점을 뜻합니다.
조금 더 이해하기 쉽게 표현하자면 인접 행렬은 2차원 배열로 N(정점의 수) X N(정점의 수) 크기의 표를 형상화하고,
정점 1과 2가 연결되어 있다면 좌표 (1, 2)와 (2, 1)에 1을 채워놓는 방식으로 정점간의 연결을 표현합니다.
여기서 처음 다뤘던 무방향, 방향, 가중치, 비가중치에 대한 내용을 잠시 복기해보겠습니다,
만약 위 그래프가 1 -> 2 방향으로 연결되어 있는 방향 그래프였다면 좌표 (1, 2)에만 1을 채우고 (2, 1)에는 1을 채우지 않도록 수정하면 될 것입니다.
또한 만약 위 그래프가 가중치가 있는 그래프였고, 1 -> 2로 이동하는 것에 4의 비용이 필요하다면, (1, 2)에 1 대신 4를 넣으면 될 것입니다.
4. 그래프의 종류
그래프는 사용되는 분야나 목적에 따라 여러 종류가 있습니다.
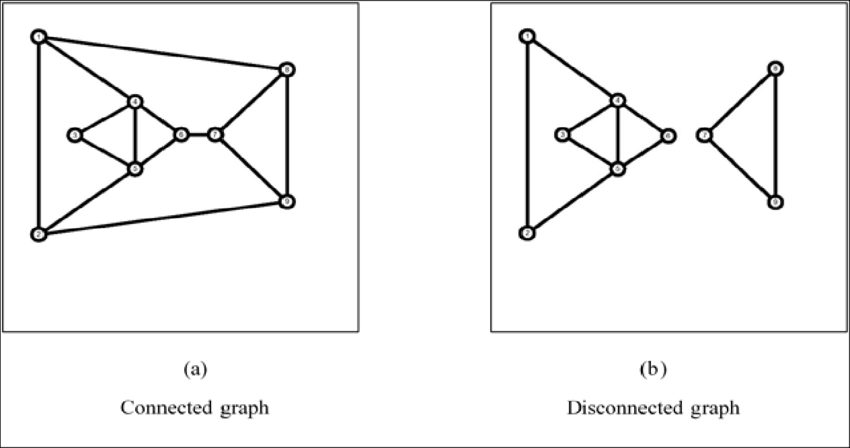
- 연결 그래프(Connected Graph): 무방향 그래프에서 모든 정점 쌍 사이에 경로가 존재하는 그래프입니다.
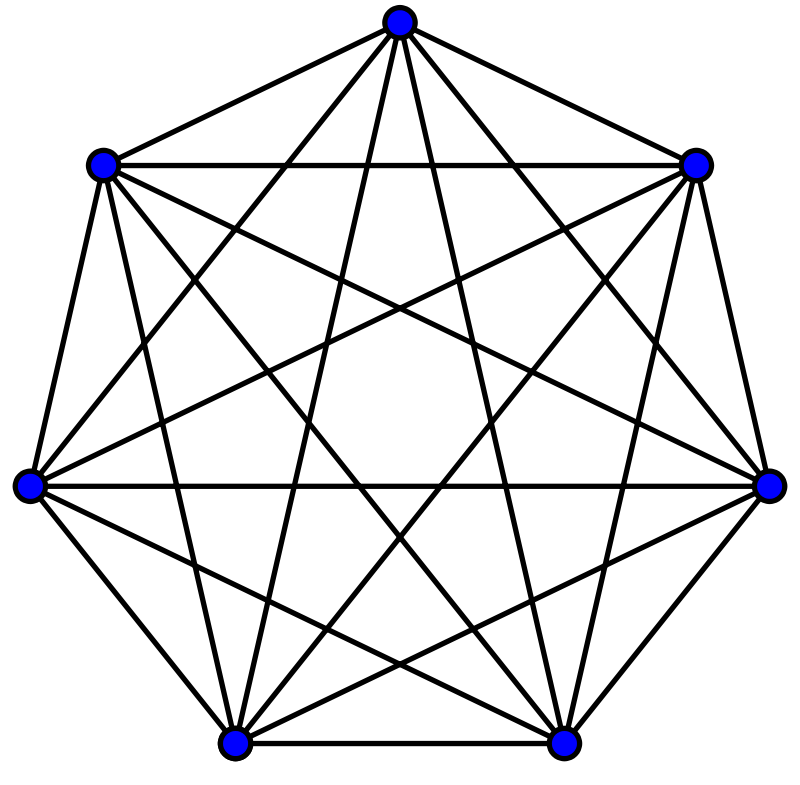
- 완전 그래프(Complete Graph): 모든 정점이 서로 직접 연결된 그래프입니다. 무방향 완전 그래프에서 정점의 수가 일 때, 간선의 수는 입니다.
- 순환 그래프(Cyclic Graph): 적어도 하나의 사이클을 포함하는 그래프입니다. 사이클은 같은 정점을 두 번 방문하지 않고 시작점으로 돌아올 수 있는 경로입니다.
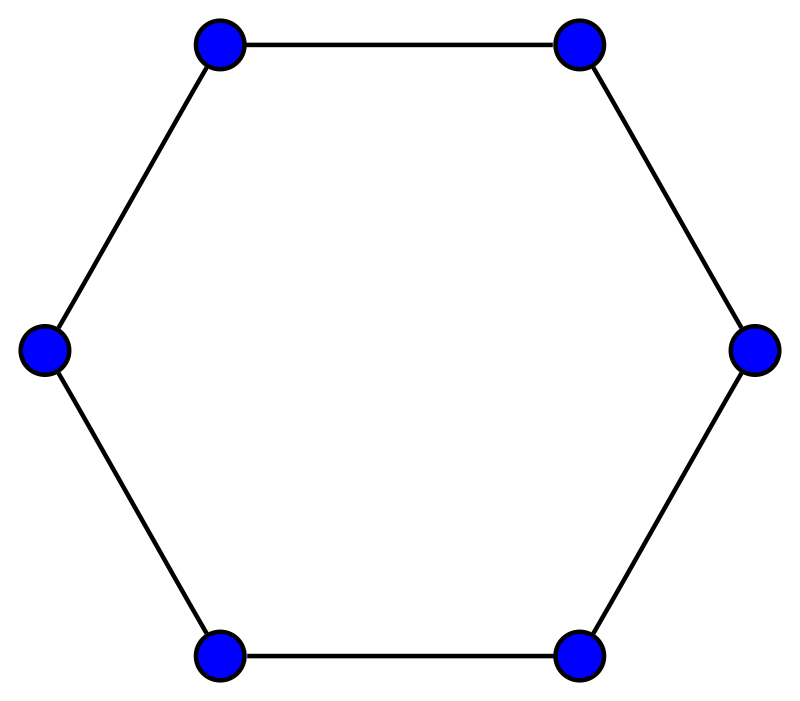
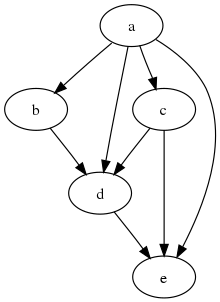
- 비순환 그래프(Acyclic Graph): 사이클이 없는 그래프입니다. 특히, 방향성이 있는 비순환 그래프를 DAG(Directed Acyclic Graph)라고 하며, 여러 최적화 문제나 데이터 구조에서 중요한 역할을 합니다.
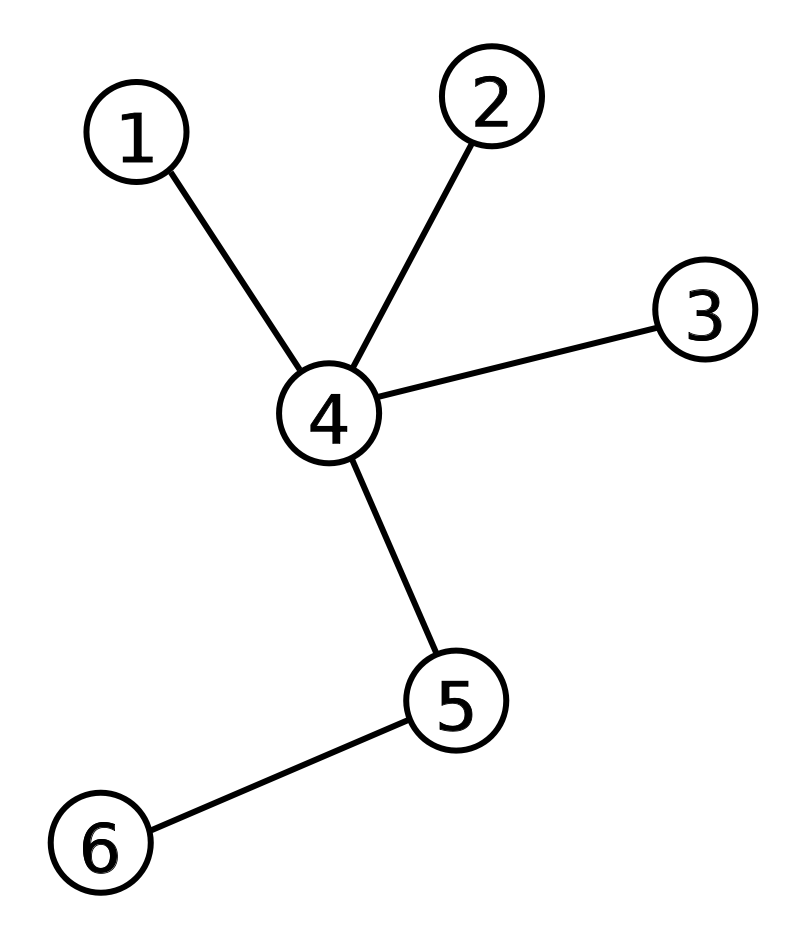
- 트리(Tree): 하나의 루트 정점을 가지고, 모든 정점이 루트 정점과 경로로 연결되어 있으며 사이클이 없는 특별한 형태의 그래프입니다.
눈치 채셨겠지만 각 종류들은 독립된 서로 다른 Graph들이 아닌 해당 특성을 나타내는 개념입니다.
이를 테면, 완전 그래프는 당연히 순환 그래프이자 연결 그래프고, 트리 또한 비순환 그래프에 포함됩니다.
그래프 이론은 그 자체로 깊고, 다양한 분야에서 응용됩니다. 특히 컴퓨터 과학, 네트워크 이론, 사회학, 생물학 등에서 그래프 이론은 복잡한 시스템을 이해하고 분석하는 데 필수적인 도구입니다.
여기까지 그래프에 대해 알아봤습니다.
내용의 오류 혹은 어색하거나 부적절한 문장을 발견하신다면, 댓글 남겨주시면 정말 감사하겠습니다.
'알고리즘 이론' 카테고리의 다른 글
| 동적 계획법 (Dynamic Programming) (0) | 2024.05.26 |
|---|---|
| LCS 알고리즘 (0) | 2024.05.24 |
| 너비 우선 탐색(BFS)와 깊이 우선 탐색(DFS) (0) | 2024.05.18 |
| 재귀 함수 (recursive function) 의 동작 (0) | 2024.04.13 |