2024. 5. 24. 14:36ㆍ알고리즘 이론
이번 포스팅에서는 LCS 알고리즘에 대해 아래의 백준 문제를 예제로 소개해보겠습니다.
https://www.acmicpc.net/problem/9251
Longest Common Subsequence / Longest Common Substring
LCS란 최장 공통 부분 수열(Longest Common Subsequence) 혹은 최장 공통 부분 문자열(Longest Common Substring)을 뜻합니다. LCS를 구하는 알고리즘은 다이나믹 프로그래밍(DP) 알고리즘의 대표적인 유형으로, 어째서 DP인지는 글의 마지막 부분에서 설명하겠습니다.
먼저 최장 공통 부분 수열( Longest Common Subsequence ) 란 두 개 이상의 시퀸스[ACAYKP, CAPCAK]가 주어졌을 때, 가장 긴 공통 부분 수열, 즉 두 문자열 모두에 존재하는 가장 긴 부분 수열(ACAK)을 뜻합니다.
그리고 최장 공통 부분 문자열 ( Longest Common Substring ) 란 두 개 이상의 문자열 [ACAYKP, CAPCAK]에 모두 속하는 부분 문자열 중 가장 긴 문자열을 뜻합니다.
두 LCS의 차이점은 수열은 중간에 다른 문자가 껴있더라도 흐름만 거스르지 않는다면 공통 부분으로 보고, 문자열에서는 중간에 다른 문자가 껴있다면 다른 부분 문자열로 판단한다는 것입니다.

두 문자열을 검사하기 위해서는 이중 중첩 for문을 통해 S1 문자의 한 문자를 잡고 S2 문자열을 순회하며 일치하는 문자의 개수를 세야하는데, 한 문자를 시작으로 연속으로 몇개의 문자가 동시에 일치하는지를 어떻게 셀 것 인지가 관건입니다.
이 문제는 두 문자열을 index로 표를 생성하여 검사를 기록하고, 특정한 규칙으로 값을 채워나가는 방식으로 해결할 수 있습니다. 최장 공통 부분 문자열 규칙과 최장 공통 부분 수열은 서로 다르며, 어떠한 이유로 어떻게 다른지를 최종적으로 확인해보며 포스팅을 마무리 하겠습니다.
최장 공통 부분 문자열 (Longest Common Substring)
1. 위 gif에서 봤듯이 이중 중첩 반복문을 사용해 두 문자열을 순회합니다.
2. 두 문자가 다르다면 LCS[i][j]에 0을 표시합니다. 두 문자가 같다면 LCS[i][j]는 LCS[i - 1][j - 1] +1이 됩니다.
*LCS 배열은 두 문자열의 길이들로 [S1.length][S2.length]로 생성한 배열이고, i, j는 문자열을 순회 중인 이중 for문의 반복 index값이다.
3. 두 문자가 같다면 LCS[i - 1][j - 1] 값을 찾아 +1 합니다.
4. 위 3번 과정을 1번 반복문 내에서 반복 수행합니다.
최장 공통 부분 수열 ( Longest Common Subsequence )
1. 위 gif에서 봤듯이 이중 중첩 반복문을 사용해 두 문자열을 순회합니다.
2. 마찬가지로 두 문자가 같다면 LCS[i - 1][j - 1] +1 의 값을 LCS[ i ][ j ] 에 넣습니다. 하지만 두 문자가 다를 경우, LCS[i][j]의 값은 0이 아닌 Math.Max(LCS[i - 1][j], LCS[i][j - 1])이 됩니다.
3. 두 문자가 같다면 LCS[i - 1][j - 1] 값을 찾아 +1 합니다.
4. 위 3번 과정을 1번 반복문 내에서 반복 수행합니다.
위 규칙들의 당위성을 지금부터 그림과 함께 자세히 살펴보겠습니다.
최장 공통 부분 문자열 (Longest Common Substring) - [ ACAYKP, CAPCAK ]

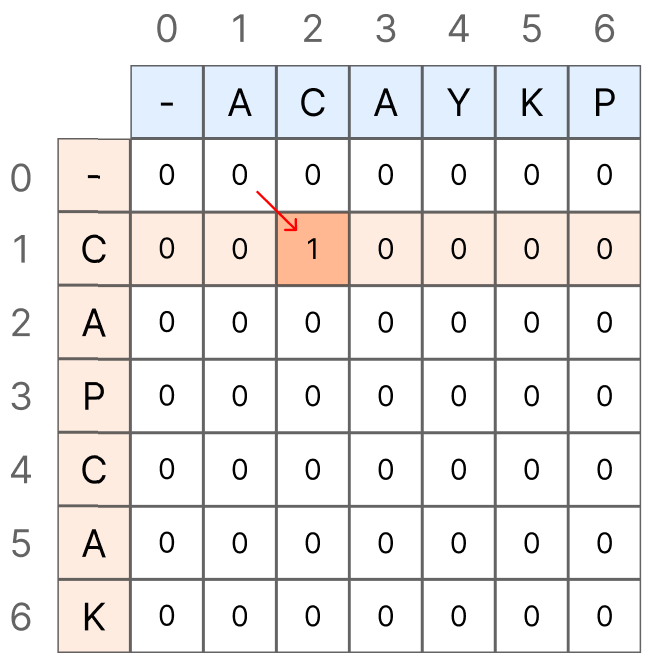
1. LCS[i - 1][j - 1]이란 속성을 사용하기 때문에 가로 세로 0번 index들을 마진값으로 채워두어야 합니다. 때문에 배열의 크기는 문자열의 길이 + 1이 됩니다. 반복문이 시작한 뒤 첫번째 문은 두번째 문자열("CAPCAK")의 첫번째 문자 C를 검사의 주체로 잡고, 첫번째 문자열("ACAYKP")를 대상으로 문자 하나씩 검사하고, 두 문자가 일치하면 LCS[i][j] 에 LCS[i - 1][j - 1] +1 값을 삽입합니다. 일치하지 않다면 0으로 둡니다.

마찬가지로 두 문자가 일치하면 LCS[i][j] 에 LCS[i - 1][j - 1] +1 값을 삽입합니다. 일치하지 않다면 0으로 둡니다.

여기서 혼동하기 쉬운 점은 실제로 현재 LCS[1][2] 의 1이 의미하는 바가 단순히 'A' 와 'A'를 비교한 것이 아닌 문자열 'A'와 'CA'의 최장 부분 문자열을 구한 것이라는 점입니다.


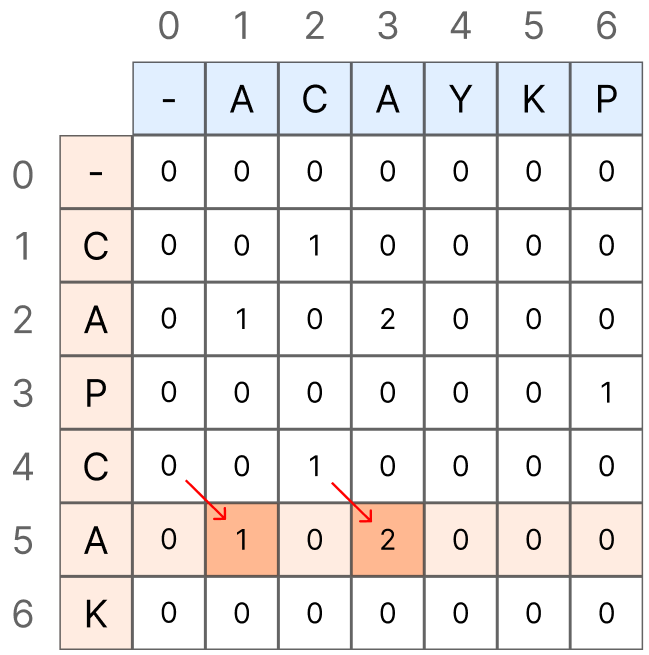

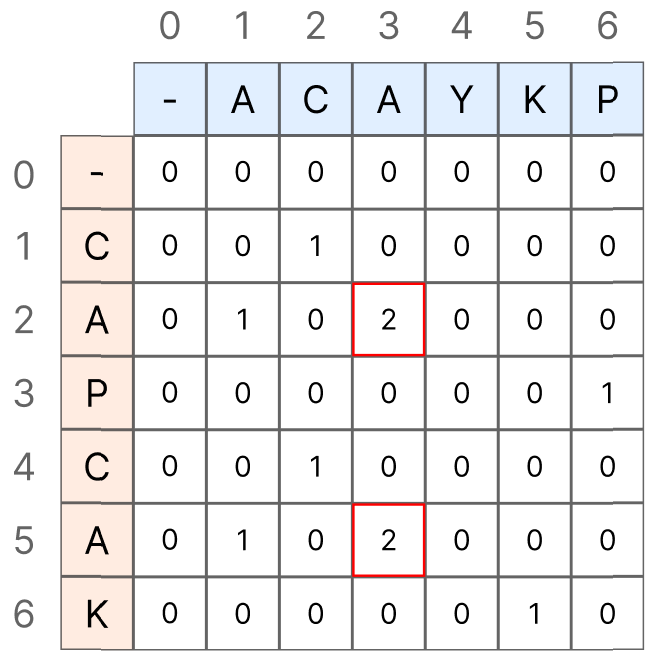
위와 같이 반복문이 모두 끝이 나면 LCS배열에는 나올 수 있는 모든 경우의 부분 수열 길이들이 채워지게 됩니다.
그리고 이 중에서 가장 큰 값이 최장 부분 문자열의 길이가 됩니다.
최장 공통 부분 수열 (Longest Common Sequence) - [ ACAYKP, CAPCAK ]
최장 공통 부분 문자열 때와 동일하게, 두 문자가 일치하면 LCS[i][j] 에 LCS[i - 1][j - 1] +1 값을 삽입합니다.
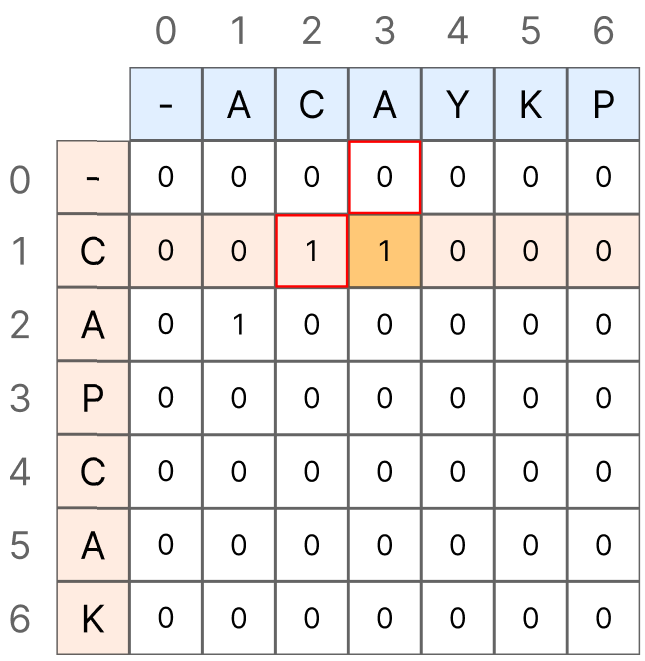
하지만 두 문자가 다를 경우, LCS[i][j]의 값은 0이 아닌 Math.Max(LCS[i - 1][j], LCS[i][j - 1])이 됩니다.
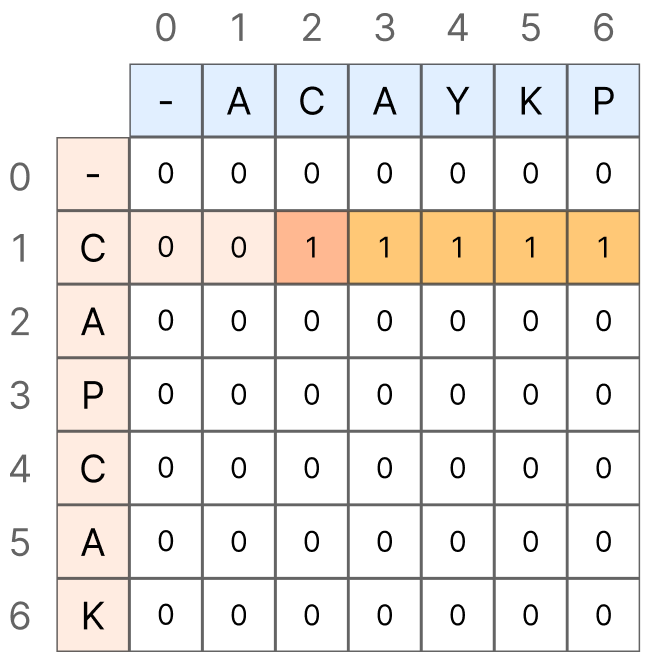
그렇기 때문에 LCS[i][j] 값은 항상 왼쪽(LCS[i][j - 1])과 위쪽 (LCS[i - 1][j]) 값보다 크거나 같음이 보장됩니다.
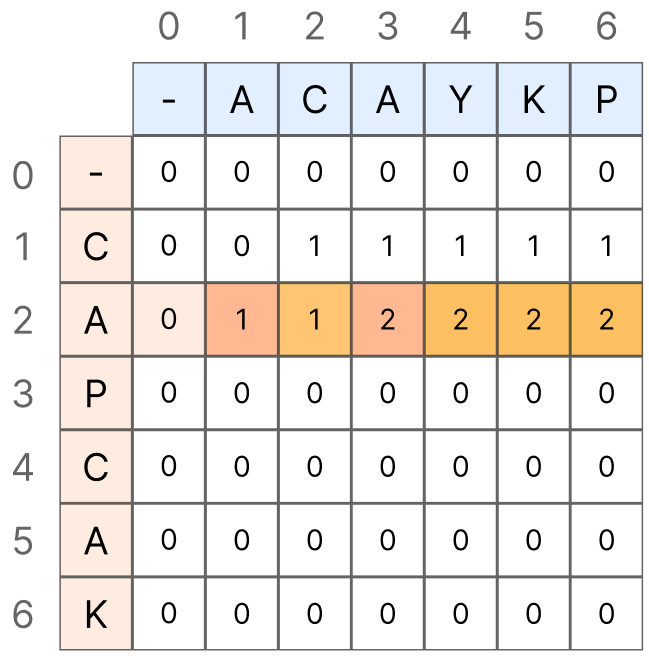

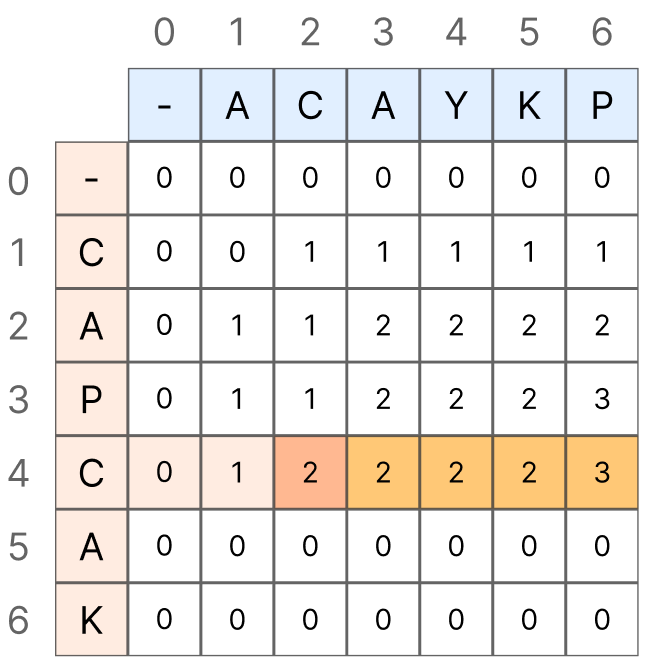

이제 공통 부분 문자열과 공통 부분 수열의 Count 방식이 왜 이런 차이점을 보이는지 알아보겠습니다.

공통 부분 문자열의 경우 CAYKP와 CAP는 다른 문자열이기 때문에 "CA"를 검사 한 뒤 Y, K를 지나는 부분에서 0으로 초기화 해주어야 합니다.
위 흐름은 실제 탐색의 흐름에서 많이 비약되었긴 하지만, 중요한 점은 연속으로 일치하지 않는다면 앞에서 검사한 일치 개수를 뒷 문자열의 일치 개수에 영향을 주어선 안된다는 것입니다.
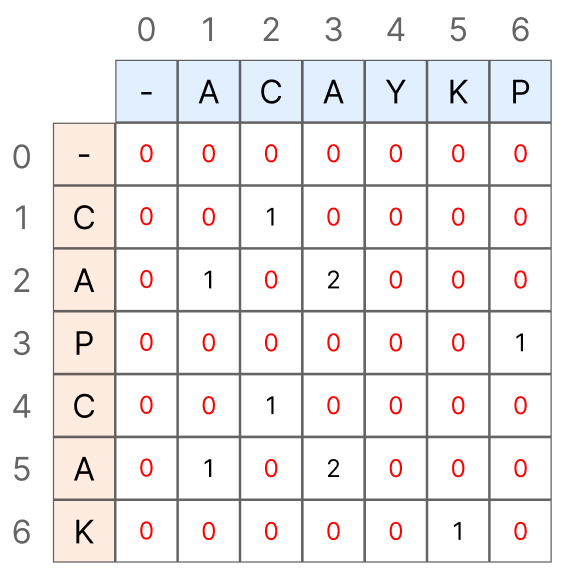
이러한 이유로 공통 부분 문자열에서는 문자가 일치 했을 때만 LCS 배열에 값이 삽입되고, 이외 경우들은 모두 값이 0인 것입니다.

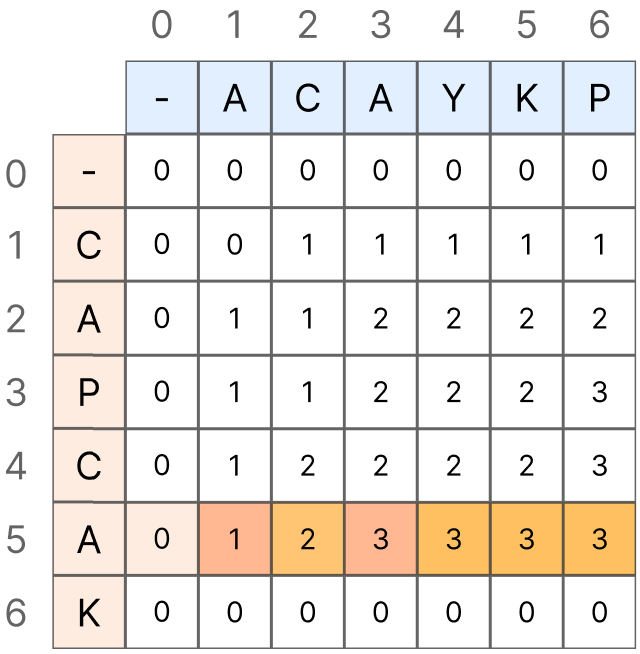
반면, 공통 부분 수열의 경우 순서만 거스르지 않는다면 CAYKP와 CAP에서 CAYKP에 존재하는 시퀸스 CAP와 CAP를 공통 부분 수열로 보기 때문에 "CA"를 검사 한 뒤 Y, K를 지나는 부분, 즉, 일치하지 않는 문자가 나오더라도 앞에서 일치했던 개수인 2를 계속해서 끌고 가주어야 합니다.

이러한 이유로 왼쪽, 혹은 위쪽 값 중 큰 값을 계속해서 가져가야 합니다. 왼쪽 값만 가져가지 않고 윗쪽 값도 고려하여 더 큰 값을 가져가는 이유는, 위 gif는 i를 기준으로 j를 순회하는 모습만 담긴 단적인 예시지만, 실제로는 index j를 기준으로도 결국엔 index i가 모두 매치되기 때문에 이에 대한 최대값도 고려하여 계속 유지해주어야 하는 것입니다.
LCS는 다이나믹 프로그래밍의 대표적인 유형입니다.
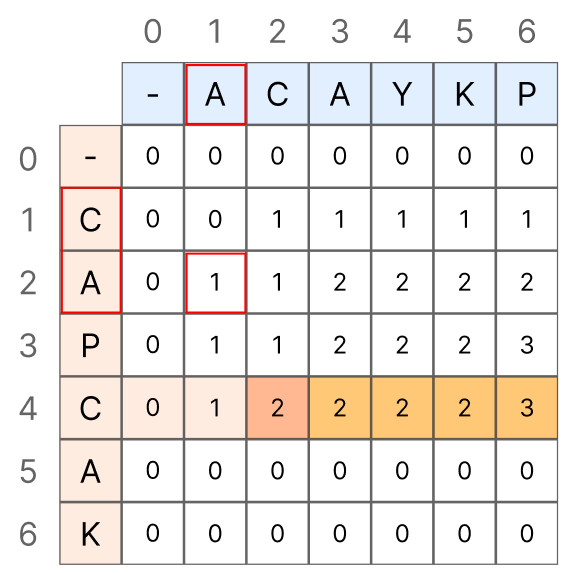


다이나믹 프로그래밍(DP)란 이렇듯 큰 문제("ACAYKP", "CAPCAK")를 작은 단위("A", "CA")로 나누어 해결하고 작은 단위에서 구한 해를 저장하여 다음 작은 단위("A", "CAP")의 문제에서, 그리고 또 다음 작은 단위("AC", "CAPC")에서 재활용하며 최종 목적까지 쌓아가는 것을 뜻합니다.
마지막으로 위 이론을 바탕으로 구현된 코드와 함께 글을 마무리하겠습니다.
//LCS
const fs = require('fs');
const [stringA, stringB] = fs
.readFileSync(0)
.toString()
.trim()
.split('\n')
.map((v) => v.replace(/\r/, '').split(''));
let LCS = new Array(stringA.length + 1)
.fill(0)
.map((v) => (v = new Array(stringB.length + 1).fill(0)));
for (let i = 1; i <= stringA.length; i++) {
for (let j = 1; j <= stringB.length; j++) {
if (stringA[i - 1] == stringB[j - 1]) {
LCS[i][j] = LCS[i - 1][j - 1] + 1;
} else {
LCS[i][j] = Math.max(LCS[i - 1][j], LCS[i][j - 1]);
}
}
}
console.log(LCS.pop().pop());
느낀점... 혼잣말
여태까지 꾸준히 느껴온 점이지만 이번 포스팅에서 특히나 체감한 부분은 내 머릿속 인사이트들을 있는 그대로 다른 사람이 쉽게 받아들일 수 있도록 글자로 풀어내는 일은 정말 어렵다는 것이다. 그래서 최대한 그림을 많이 사용하려 했고, 그럼에도 아쉬움이 많이 남았다. 하지만 다른 사람을 더 쉽게 이해시키려는 이러한 고민들이 미래에 팀원, 상사들과 갖게 될 커뮤니케이션에서 크게 도움 될 것 같다 느꼈다.
'알고리즘 이론' 카테고리의 다른 글
| 동적 계획법 (Dynamic Programming) (0) | 2024.05.26 |
|---|---|
| 너비 우선 탐색(BFS)와 깊이 우선 탐색(DFS) (0) | 2024.05.18 |
| 재귀 함수 (recursive function) 의 동작 (0) | 2024.04.13 |
| 그래프 ( Graph ) 탐색 이론 (1) | 2024.03.29 |