2024. 6. 4. 15:21ㆍ코딩 테스트 (BOJ)
https://www.acmicpc.net/problem/10986
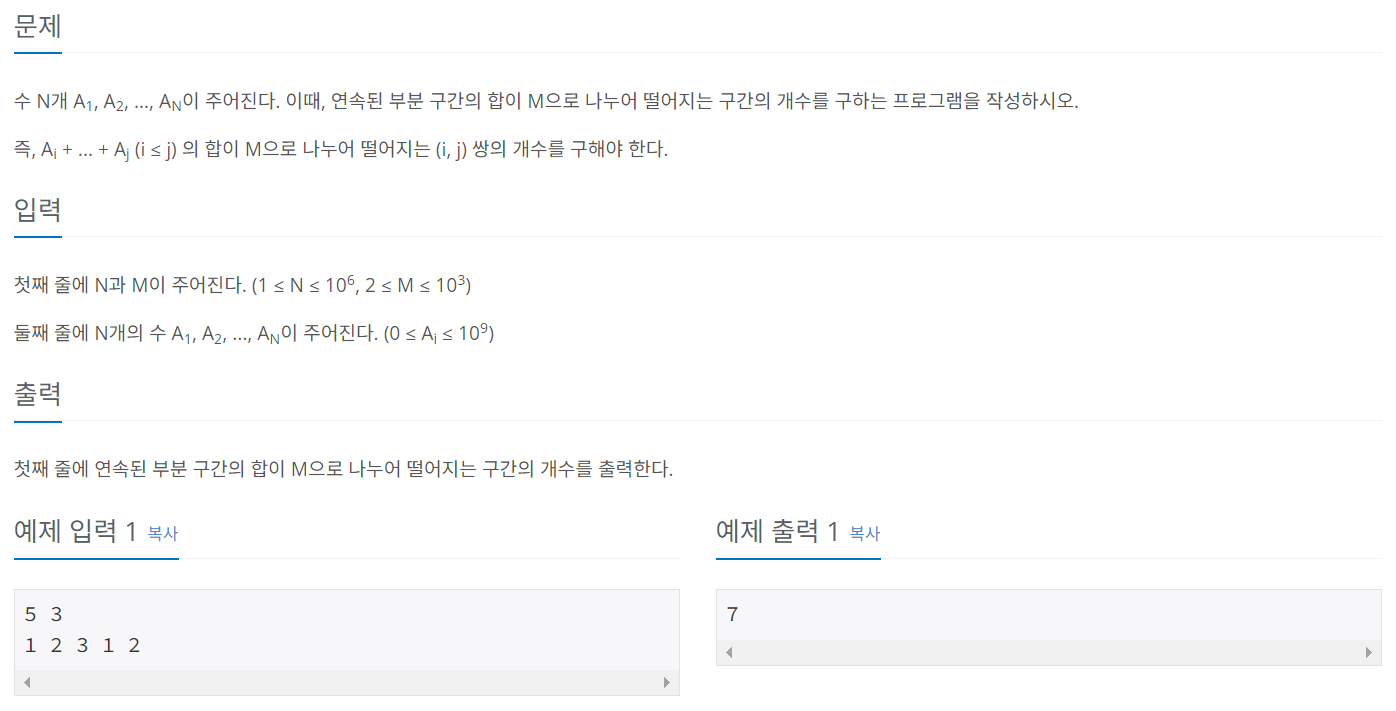
누적합(prefix sum)
먼저 누적합이란 나열된 수의 누적된 합을 말한다. 만약 [1, 2, 3, 4, 5] 라는 배열이 있고, 이 배열을 누적합으로 나타낸다면 [1, 3, 6, 10, 15] 가 된다.
보통 반복문을 통해 `0번 index부터 4번 index까지의 누적합`을 구한다면 5번의 수행동작이 필요하다. 즉 O(N)의 시간 복잡도를 갖는 것이다. 하지만 누적합을 사용하여 `0번 index부터 4번 index까지의 누적합`을 구한다면 누적합 배열의 4번 index 값을 꺼내오기만 하면 되기 때문에 O(1)의 시간 복잡도를 갖는다.
그렇다면 `2번 index부터 4번 index까지의 누적합`을 구하기 위해서는 어떻게 해야할까? (1 + 2 + 3 + 4 + 5)[0 ~ 4] 에서 (1 + 2)[0 ~ 1]을 빼주면 (3 + 4 + 5)[2 ~ 4]가되기 때문에 누적합 배열 4번 인덱스 값 15에서 1번 인덱스 값 3 을 빼주면 된다.
문제 풀이
처음에는 이중 for문의 i와 j를 완전 탐색하여 누적합의 i번째 index의 값에서 j번째 index값을 빼주는 방식으로, j ~ i의 구간합이 m으로 나누어 떨어지는지 검사하였다. 하지만 수의 개수가 최대 10억개이기 때문에 당연히 시간초과가 발생했다.
//나머지 합
const fs = require('fs');
const [[N, M], arr] = fs
.readFileSync(0)
.toString()
.trim()
.split('\n')
.map((item) => item.split(' ').map((v) => +v));
let prefix_sums = Array(N);
prefix_sums = [...arr];
//누적합 배열 생성
for (let i = 1; i < N; i++) {
prefix_sums[i] = prefix_sums[i] + prefix_sums[i - 1];
}
let cnt = 0;
//M으로 나누어 떨어지는 구간합 탐색
for (let i = 0; i < N; i++) {
if (prefix_sums[i] % M === 0) cnt++;
for (let j = 0; j < i; j++) {
if ((prefix_sums[i] - prefix_sums[j]) % M === 0) {
cnt++;
}
}
}
console.log(cnt);
그렇기 때문에 모든 구간합에 대해 검사하지 않기 위해서 한가지 아이디어가 더 필요했다. 그 아이디어는 다음과 같다.
세개의 수 N, K, M에 대하여 N % M === K % M 일 경우 (N - K)는 M으로 나누어 떨어진다.
예시) N이 23이고, K가 28, M이 5라고 가정했을 때, N % M 과 K % M의 값은 3으로 동일
N은 (20 + 3), K는 (25 + 3)으로 나타 낼 수 있는데, N(20 + 3) - K(25 + 3)을 하게 될 경우 나머지인 3이 소거되기 때문이다.
이러한 이유로 j부터 i까지의 구간합 prefix_sum[i] - prefix_sum[j] 에 대해서
prefix_sum[i] % m === prefix_sum[j] % m 이라면 prefix_sum[i] - prefix_sum[j]은 m으로 나누어 떨어진다. 즉, j부터 i까지의 구간합이 m으로 나누어 떨어진다.
이제 위 식을 사용하기 위해서 누적합의 각 index 별 M으로 나누었을 때의 나머지 값들을 모두 저장해두고 같은 나머지 값을 갖는 누적합끼리 같은 집합으로 묶는다. 그리고 각 집합 별 전체 원소 n개 중 2개의 원소를 뽑아내는 경우의 수 nC2를 구하고, 집합 별 nC2들을 모두 더해주면 0으로 나누어 떨어지는 모든 경우의 수를 구할 수 있다.
실제 값을 대입하여 살펴보자.
Ex) prefix_sum = [1, 3, 6, 10, 15] 에 대하여 2로 나누었을 때
나머지가 0이 나오는 수의 개수 2개 {6, 10} // (10 - 6)은 2로 나누어 떨어짐, 10 - 6은 index 3부터 4까지의 구간합
나머지가 1이 나오는 수의 개수 3개 {1, 3, 15} // (3 - 1), (15 - 3), (15 - 1) 모두 2로 나누어 떨어짐
{6, 10} 에서 두개의 원소를 뽑아내는 경우의 수 === 2C2
{1, 3, 15} 에서 두개의 원소를 뽑아내는 경우의 수 === 3C2
2C2 + 3C2 = 1 + 3 = 4
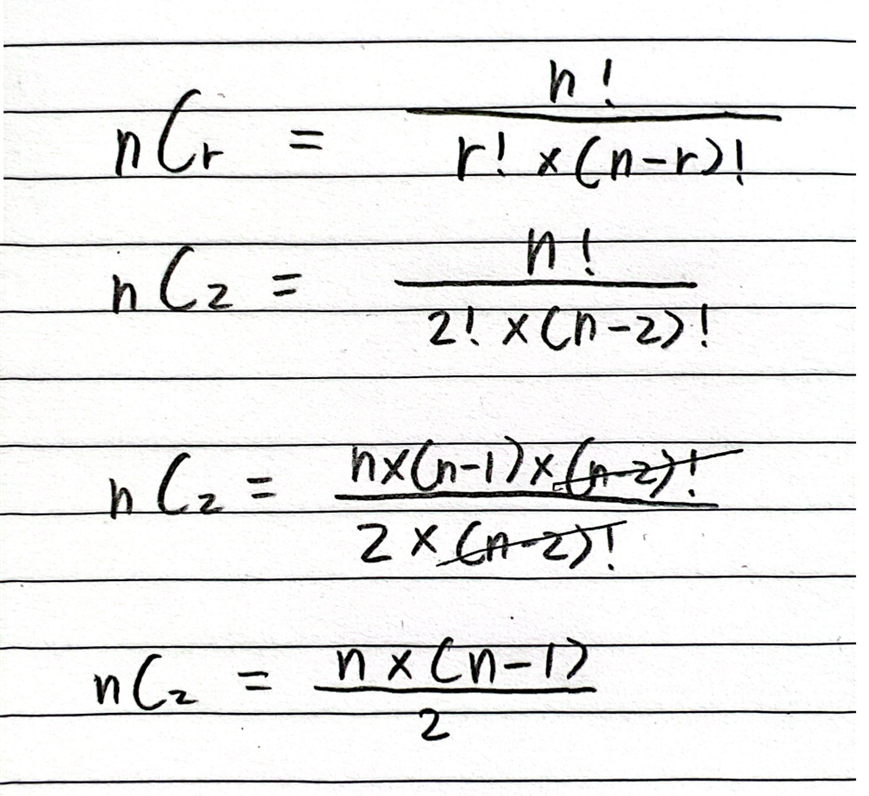
그리고, nC2의 경우 위와 같이 식을 정리할 수 있기 때문에 팩토리얼이 필요없이 n * (n - 1)이란 식만으로 값을 구할 수있다.
전체코드
//나머지 합
const fs = require('fs');
const [[N, M], arr] = fs
.readFileSync('../input.txt')
.toString()
.trim()
.split('\n')
.map((item) => item.split(' ').map((v) => +v));
let prefix_sums = Array(N);
prefix_sums = [...arr];
let map = new Map();
let cnt = 0;
if (prefix_sums[0] % M === 0) {
cnt++;
}
map.set(prefix_sums[0] % M, 1);
// M으로 나누었을 때 나머지 값 r의 집합
// expected : {나머지 : 개수, 1 : 3, ...}
for (let i = 1; i < N; i++) {
prefix_sums[i] = prefix_sums[i] + prefix_sums[i - 1];
let mod = prefix_sums[i] % M;
if (!mod) {
cnt++;
}
if (map.has(mod)) {
map.set(mod, map.get(mod) + 1);
} else {
map.set(mod, 1);
}
}
// nC2
map.forEach((value) => {
cnt += (value * (value - 1)) / 2;
});
console.log(cnt);
'코딩 테스트 (BOJ)' 카테고리의 다른 글
| [백준 / BOJ] 11444번 피보나치 수 6 (Javascript / Node js) (1) | 2024.06.04 |
|---|---|
| [백준 / BOJ] 17114번 하이퍼 토마토 (Javascript / Node js) (0) | 2024.05.26 |
| [백준 / BOJ] 7576번 토마토 ( Node js / Javascript ) (0) | 2024.05.22 |
| [백준 / BOJ] 1107번 리모컨 ( Node js / Javascript ) (1) | 2024.03.29 |
| [백준 / BOJ] 1074번 Z ( Javascript / Node js ) (0) | 2024.03.22 |