2024. 6. 4. 13:15ㆍ코딩 테스트 (BOJ)
https://www.acmicpc.net/problem/11444

인사이트
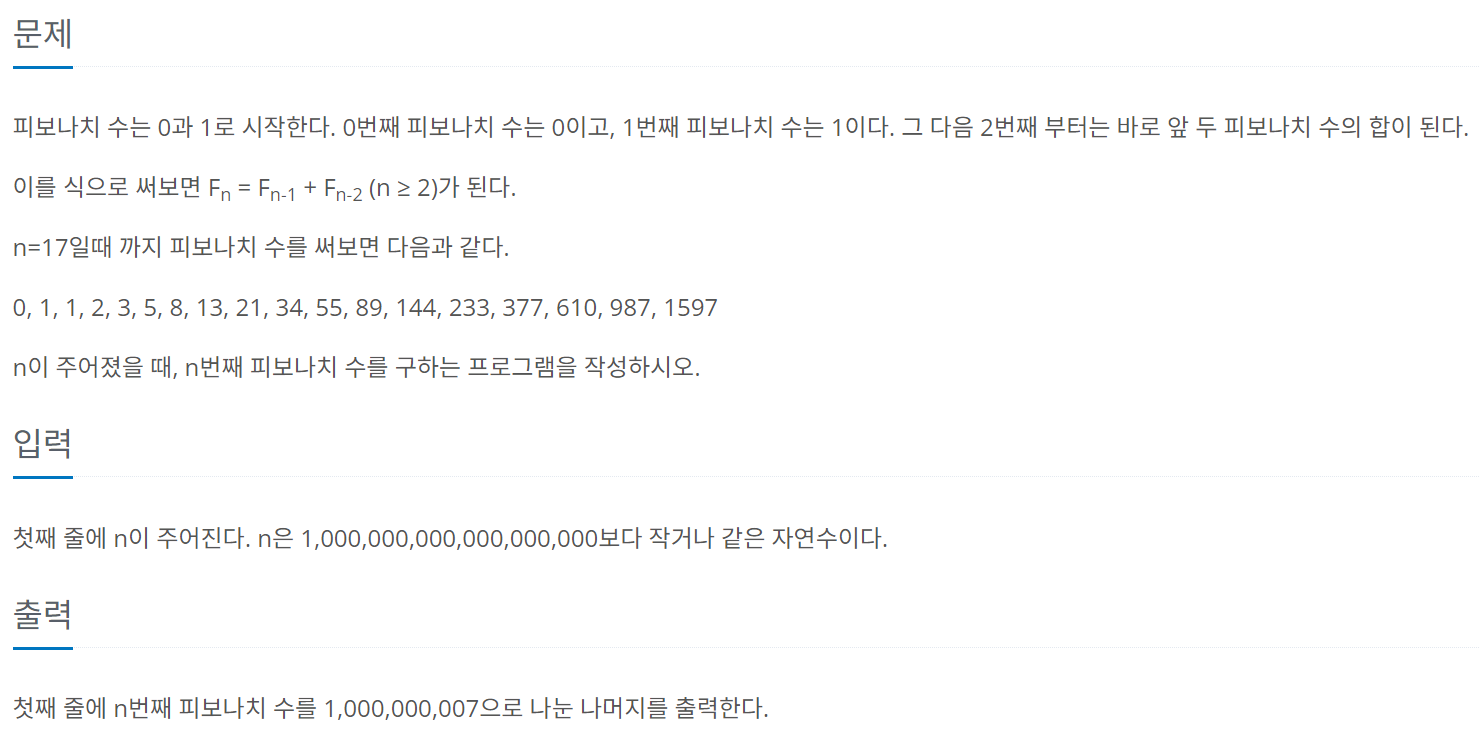
이번 문제는 우리들이 사랑하는 피보나치 수열이다. 피보나치 수열이 골드2까지 난이도가 책정된 이유에는 입력값의 크기 제한에 있다.
일반적으로 1초에 대략 1억번 정도의 연산이 처리된다는 것을 감안하면, 입력값의 최대값이 1000억이기 때문에 dp를 사용해서 O(N)의 시간 복잡도로 처리해도 시간 초과가 날 것임을 예상할 수 있다.
그렇기 때문에 피보나치 수열의 일반항으로는 어떤 짓을 해도 시간초과를 해결할 수 없을 것이다. 해서, 이 피보나치 수열의 일반항에서 시간 처리를 극적으로 줄일 점화식을 고안해내야 한다. 여기서 한가지 더 생각해보면 1000억이란 숫자를 1억 내로 안정적으로 줄이려면 제곱근으로 접근하는 것 외에는 거의 방법이 없을 것임을 생각해볼 수 있다.
사실은 이러한 인사이트는 추후에 든 생각이고, 처음에는 막연히 식을 풀어봤었다.
문제 풀이

피보나치 수열의 일반항은 `F(n) = F(n-1) + F(n-2)` 다. 그리고 같은 식으로 `F(n-1) = F(n-2) + F(n-3)` 이다. 때문에, 일반항 `F(n) = F(n-1) + F(n-2)`의 F(n-1)이 F(n-2) + F(n-3)으로 치환이 가능함으로 `F(n) = 2F(n-2) + F(n-3)`이 성립한다.
다시 마찬가지로 F(n-2) = F(n-3) + F(n-4)로 치환이 가능하고 이 과정을 반복하다 보면, F(n) 을 다음과 같은 식들로 표현이 가능하다.
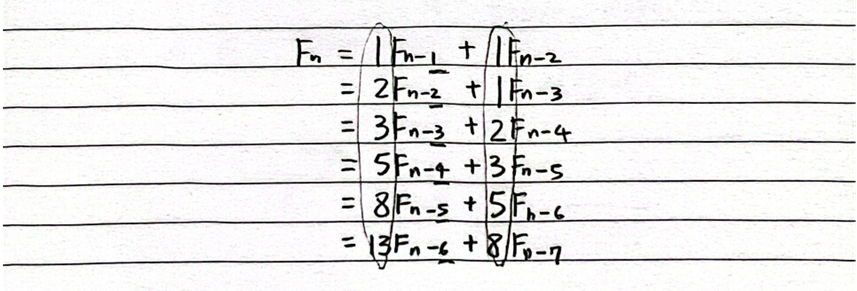
그런데 각 F(n-k) 와 F(n-k-1) 앞의 상수를 살펴보면 마찬가지로 피보나치 수열을 이루고 있는 것을 알 수 있다. (여기서 k는 `F(n) = F(n-1) + F(n-2)` 에서 1과 2를 뜻함)
그리고 이 피보나치 수열이 F(n-k) 앞의 상수는 피보나치 수열 F(k + 1)이고 F(n-k-1) 앞의 상수는 F(k)라는 것까지 알아낼 수 있다. 이제 식 `F(n) = F(k+1) * F(n-k) + F(k) * F(n-k-1)` 이 된다.
그럼 이제 F(n)의 n에 k를 대입하면 일반항을 k로 재정립할 수 있게 된다. 하지만 F(n-k)와 F(n-k-1)을 고려하여 2k를 넣도록 하자. 그럼 최종적으로 아래와 같이 식이 정리된다. + (n 에 k-1을 넣으면 원래의 피보나치 수열의 일반항으로 돌아간다. 수학은 정말 신비롭다.)

하지만 위 식은 2k에 대한 식이므로 짝수의 경우만 구할 수 있기 때문에 홀수에 대한 식을 추가로 세워야 한다. 홀수의 경우는 n에 2k+1을 넣는 것으로 하자.
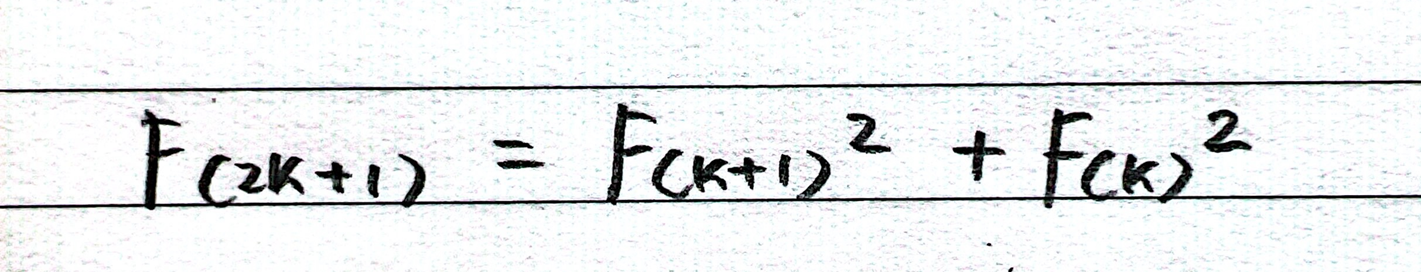
처음 목표로 했던 좌변의 대입값을 제곱으로 표현하는 것에 성공했다. 이제 위 두 식을 이용해 짝수와 홀수의 경우를 분할하여 각각 재귀적으로 구하면 되겠다. 당연히 입력값이 1000억이나 되니 구한 값은 메모이제이션하여 dp의 TopDown 방식으로 구해내면 되겠다.
아래는 구현한 코드이다.
const fs = require('fs');
const mod = 1000000007n;
const N = BigInt(fs.readFileSync('../input.txt').toString().trim());
let memo = new Map();
const fibo = (N) => {
if (N === 0n) return 0n;
if (N === 1n) return 1n;
if (N === 2n) return 1n;
if (memo[N] > 0n) return memo[N];
if (N % 2n === 0n) {
memo[N] = (fibo(N / 2n) * (fibo(N / 2n + 1n) + fibo(N / 2n - 1n))) % mod;
}
if (N % 2n === 1n) {
memo[N] = (fibo((N + 1n) / 2n) ** 2n + fibo((N - 1n) / 2n) ** 2n) % mod;
}
return memo[N];
};
console.log(fibo(N).toString().replace('n', ''));'코딩 테스트 (BOJ)' 카테고리의 다른 글
| [백준 / BOJ] 10986번 나머지 합 (Javascript / Node js) (1) | 2024.06.04 |
|---|---|
| [백준 / BOJ] 17114번 하이퍼 토마토 (Javascript / Node js) (0) | 2024.05.26 |
| [백준 / BOJ] 7576번 토마토 ( Node js / Javascript ) (0) | 2024.05.22 |
| [백준 / BOJ] 1107번 리모컨 ( Node js / Javascript ) (1) | 2024.03.29 |
| [백준 / BOJ] 1074번 Z ( Javascript / Node js ) (0) | 2024.03.22 |