2024. 1. 9. 15:06ㆍ코딩 테스트 (BOJ)
https://www.acmicpc.net/problem/1932
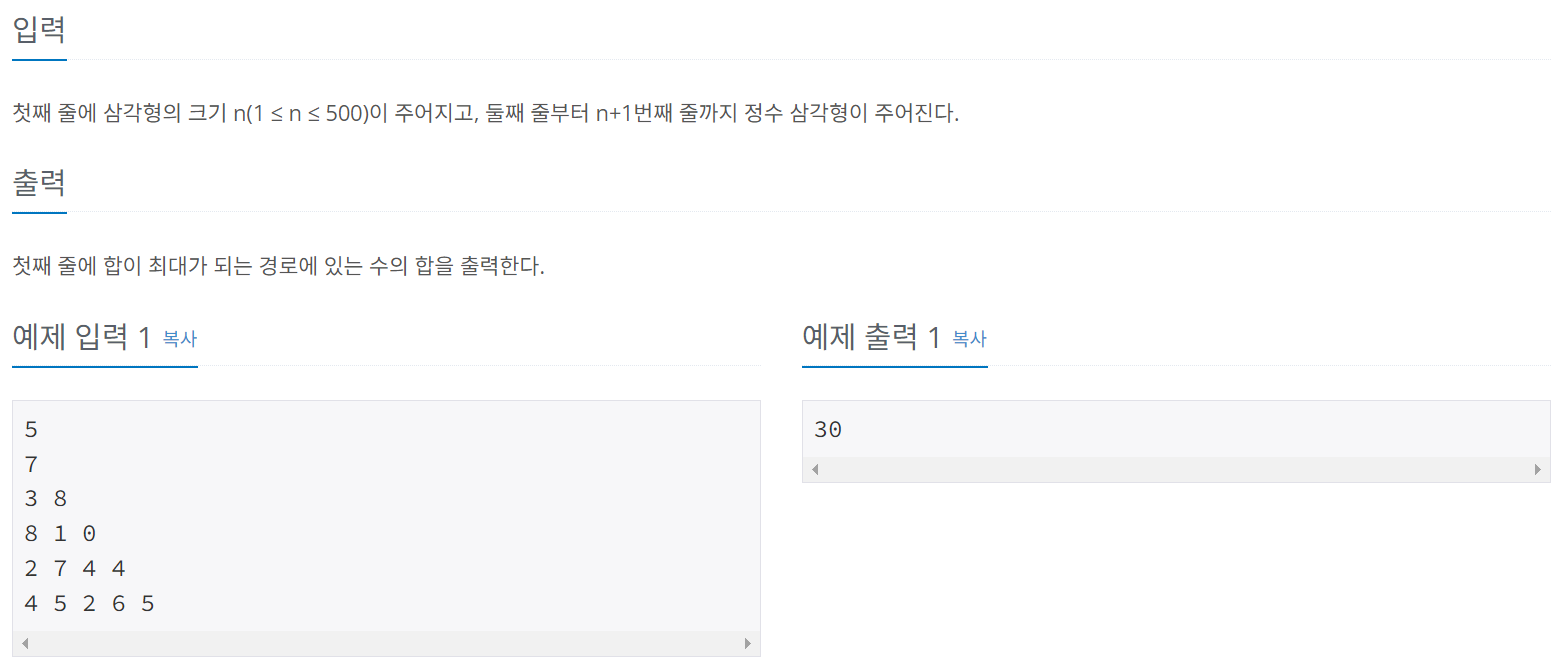
1932번: 정수 삼각형
첫째 줄에 삼각형의 크기 n(1 ≤ n ≤ 500)이 주어지고, 둘째 줄부터 n+1번째 줄까지 정수 삼각형이 주어진다.
www.acmicpc.net

위 문제는 전형적인 동적 계획법 (Dynamic Programming), DP 문제이다. 동적 계획법(DP)의 정의는 큰 문제를 작은 문제로 나누어 푸는 방식을 말한다.
큰 문제를 작은 문제로 나누어 푸는 방식을 동적 계획법(DP)이라고 부른다면 분할과 정복과 어떤 차이가 있는지 궁금할 수 있다.
가장 큰 차이점은 동적 계획법은 분할과 정복과 다르게 하위 문제의 해결이 상위 문제에서 사용 되기 때문에, 하위 문제의 해결을 재사용한다는 것이다. 그리고 이렇게 하위 문제를 재사용하기 위해 저장하고, 상위 문제에서 저장된 하위 문제를 재사용하는 방식을 Memoization(메모이제이션) 기법이라고 한다.
나는 개인적으로 DP 문제를 풀때는 항상 막연하게 먼저 식을 세워본다. 왜냐하면 세워진 식을 통해 규칙을 발견하고 점화식이 세워지거나, 혹은 바로 일반항이 구해지기도 하기 때문이다. 아래는 내가 이번 문제를 풀 때 의식의 흐름을 나타낸 것이다.
문제에서 제공된 입력 예제에서 마지막 줄만 제외하여 풀이했다. 우선 삼각형을 배열로 저장했다. 배열은 a[ x ][ y ] 형태이며, 그 예로 1은 배열 a[ 2 ][ 1 ]에 저장된다.
| index(x\y) | 0 | 1 | 2 | 3 |
| 0 | 7 | |||
| 1 | 3 | 8 | ||
| 2 | 8 | 1 | 0 | |
| 3 | 2 | 7 | 4 | 4 |
위 배열을 통해 문제를 좀 더 직관적으로 나타내면 아래와 같다.
7 (a[0][0])
3 (a[1][0]) <- 7 (a[0][0])
8 (a[1][1]) <- 7 (a[0][0])
8 (a[2][0]) <- 3 (a[1][0])
1 (a[2][1])<- 3 (a[1][0]), 8 (a[1][1])
0 (a[2][2])<- 8 (a[1][1])
2 (a[3][0]) <- 8 (a[2][0])
7 (a[3][1]) <- 8 (a[2][0]) , 1 (a[2][1])
4 (a[3][2]) <- 1 (a[2][1]) , 0 (a[2][2])
4 (a[3][3]) <- 0 (a[2][2])
그리고 규칙을 찾기위해 불필요한 실제 수들은 지웠다.
a[0][0]
a[1][0] <- a[0][0]
a[1][1] <- a[0][0]
a[2][0] <- a[1][0]
a[2][1] <- a[1][0], a[1][1]
a[2][2] <- a[1][1]
a[3][0]) <- a[2][0]
a[3][1]) <- a[2][0] , a[2][1]
a[3][2]) <- a[2][1] , a[2][2]
a[3][3]) <- a[2][2]
위에까지는 모든 경우의 경로들을 나타낸 것이고, 문제는 최대값의 경우를 찾아내야 하니, 아래와 같이 식을 세울 수 있다.
a[0][0]
a[1][0] <- Max( a[0][0] )
a[1][1] <- Max( a[0][0] )
a[2][0] <- Max( a[1][0] )
a[2][1] <- Max( a[1][0], a[1][1] )
a[2][2] <- Max( a[1][1] )
a[3][0]) <- Max( a[2][0] )
a[3][1]) <- Max( a[2][0] , a[2][1] )
a[3][2]) <- Max( a[2][1] , a[2][2] )
a[3][3]) <- Max( a[2][2] )
a[ i ][ j ] = Max( a[ i - 1 ][ j - 1 ] , a[ i - 1][ j ] )
이렇게 나온 일반항을 사용하면 삼각형의 맨 아래 부분( 2, 7, 4, 4 )에서 각각 나올 수 있는 최대값의 경우의 수들을 전부 구할 수 있다. 그리고 마지막으로 최대값의 경우의 수들 중의 최대값을 구하면 문제가 해결된다.
전체 코드
const fs = require("fs");
const input = fs
.readFileSync("../input.txt")
.toString()
.trim()
.split("\n")
.map((v) => v.split(" ").map((item) => Number(item)));
const n = input.shift();
let dp = [...input];
for (let i = 1; i < dp.length; i++) {
for (let j = 0; j < dp[i].length; j++) {
if (j == 0) {
dp[i][j] += dp[i - 1][j];
} else if (j == dp[i].length - 1) {
dp[i][j] += dp[i - 1][j - 1];
} else {
dp[i][j] += Math.max(dp[i - 1][j - 1], dp[i - 1][j]);
}
}
}
console.log(Math.max(...dp[dp.length-1]));'코딩 테스트 (BOJ)' 카테고리의 다른 글
| [백준 / BOJ] 1012번 유기농 배추 ( Javascript / Node js ) (1) | 2024.03.20 |
|---|---|
| [BOJ / 백준] 18111번 마인크래프트 ( Node js / Javascript ) (0) | 2024.03.15 |
| [백준 / BOJ] 24060번 알고리즘 수업 - 병합 정렬 1 (Javascript / Node js) (0) | 2023.11.21 |
| [백준 / BOJ] 18258번 큐 2 ( Node js / Javascript) (0) | 2023.11.02 |
| [백준/BOJ] 12789번 도키도키 간식드리미 (Javascript / Node js) (2) | 2023.10.31 |